6-2 . 2 단계 - S + Jδ 틀 완성시키기  ( T2, T3 , T7, T8 완성 )

 S + Jδ 틀이란 S 와 δ로 이루어져 있으며 T2, T3 , T7, T8 귀문을 완성시킨다.

 실제 값을 대입하면서 S + Jδ 틀을 만들어 보자.

① δ 값 정하기  ( δ = J4 + J5 + J10 + J11 )

    S값을 정하기 전에 δ 값을 먼저 정해야 일이 수월하다.

    δ 값은 반드시 베타-델타공식을 만족하도록 정해야 한다.

     베타-델타 공식과 이미 정한 베타값을 고려하여 델타값을 정해보자.

       δ = 465 - 4x - β = 465 - 4*100 - 31 = 34

    C 틀 만들 때 이미 사용된 8개의 숫자를 제외한 나머지 22 개의 숫자중에서

    합이 34 가 되는 수들은 아래처럼 상당히 많이 존재한다.

       34  = 1 +  2  +  3  +  28

            = 1 +  2  +  4  +  27  

             .....

            = 2 + 9 + 12 + 13

이 중에서 마음이 가는대로 적당히 골라서 δ 값을 정하면 된다.

여기서는 2 + 6 + 9 + 17 을 δ 값으로 정해보자.

δ 값으로 정해진 네 개의 숫자는 J4, J5, J10, J11 에 알맞게 배정될 것이다.

② S 값 정하기 ( S = S1 + ..... + S8 )

이미 정해진 12 개의 숫자를 제외한 18 개 중에서 S 값으로 8 개를 정한다.

물론 이 경우 CS 공식을 반드시 만족하도록 정해야만 한다.

C = α + β + γ = (10 + 11) + (15 + 16) + ( 8 + 14 + 20 + 27 ) = 121 이므로

CS공식에 대입하면 아래처럼 S값이 계산된다.

       S = 9x - 465 - 2C = 9*100 - 465 - 2*121 = 193

합이 193이 되는 8개의 수를 골라서 S 라고 정하면 된다.

이미 사용된 12개 숫자와 겹치지 않게 S를 정해야한다.

아래처럼 30개 숫자를 다 써놓고 이미 사용된 숫자는 괄호로 처리했다.

괄호속에 있는 이미 사용된 숫자를 제외하고 합이 193이 되도록 8개를 골라서 S 로 삼는다.

  1        (2)      3      4      5      (6)     7      (8)    (9)    (10)   (11)    12     13   (14)   (15)

  (16)    (17)    18    19    (20)    21      22     23     24     25      26    (27)    28    29    30

사용할 수 있는 숫자 18개 중에서 합을 193 으로 만드는 8개의 숫자쌍이 상당히 많다.

그 중에서 마음이 내키는대로 아래처럼 S 값을 정했다.

  S = 18 + 19 + 21 + 22 + 26 + 28 + 29 + 30 = 193

S가 정해지고 나면 10 개의 숫자가 남는데 이들은 자동적으로 ε(입실론) 값이 되며 J 꼭지점에 해당된다.

위의 경우 남은 10개의 값은 아래와 같다.

  ε = 1 + 3 + 4 + 5 + 7 + 12 + 13 + 23 + 24 + 25 = 117

이제 C, S, J 꼭지점에 배당될 숫자들이 완전히 분류되었다.

또한 α, β, γ, δ, ε 에 배정될 숫자까지 다 정해졌으므로 반은 완성된 셈이다.

지금까지 정해진 C, S, J 와 세부적인 α, β, γ, δ, ε 의 값은 아래와 같다.

     C = α + β + γ = 21 + 31 + 69 = 121

          α = C1 + C8 = 10 + 11 = 21

          β = C2 + C7 = 15 + 16 = 31

          γ = C3 + C4 + C5 + C6 = 8 + 20 + 14 + 27 = 69

     S = 18 + 19 + 21 + 22 + 26 + 28 + 29 + 30 = 193

     J = δ + ε = 34 + 117 = 151

         δ = 2 + 6 + 9 + 17 = 34

         ε = 1 + 3 + 4 + 5 + 7 + 12 + 13 + 23 + 24 + 25 = 117

맞게 분류되었는지 확인해보자.

1 에서 30 까지의 합이 465  이므로 C + S + J 값도 465 가 되어야 한다.

  C + S + J = 121  + 193 + 151 = 465

C, S, J 의 합이 465 를 가지므로 C , S , J 값이 맞게 분류되었다.

이제부터는 S와 J값을 적당히 조절하면 된다.

③ S + Jδ 틀 만들기

S + Jδ 틀은 T2, T3,  T7, T8를 이루는 중간단계에 있는 귀문들로 구성되며

각 귀문들은 3개의 C , 2개의 S , 한 개의 J 꼭지점으로 이루어져있다.

C 꼭지점들은 이미 1단계에서 숫자들이 채워져있다.

나머지 S 꼭지점 2개와 J 꼭지점 한 개를 채우면 된다.

S 와 δ 에 들어갈 숫자들은 이미 정해져 있으며 x=100을 만족하도록 적절히 배치를 하면 된다.

숫자들을 배치할 때 좀더 쉽게 하기 위해서 아래 그림처럼 정의한다.

  ㄱ = S1 + J4 + S3

  ㄴ = S2 + J5 + S4

  ㄷ = S5 + J10 + S7

  ㄹ = S6 + J11 + S8

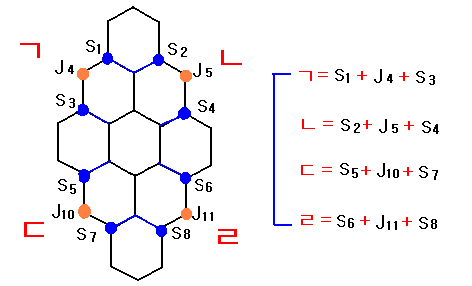
그러면 ㄱ, ㄴ, ㄷ, ㄹ 을 결정해보자.

ㄱ, ㄴ, ㄷ, ㄹ은  S에 지정된 숫자 8개 중에서 2개와 델타에 지정된 숫자 4개 중에서 한 개로 구성된다.

아무 숫자나 되는 것이 아니라 100을 만들 수 있도록 조건에 맞는 숫자만 해당된다.

아래 그림에 ㄱ, ㄴ, ㄷ, ㄹ의 값을 구하는 방법이 나타나있다.

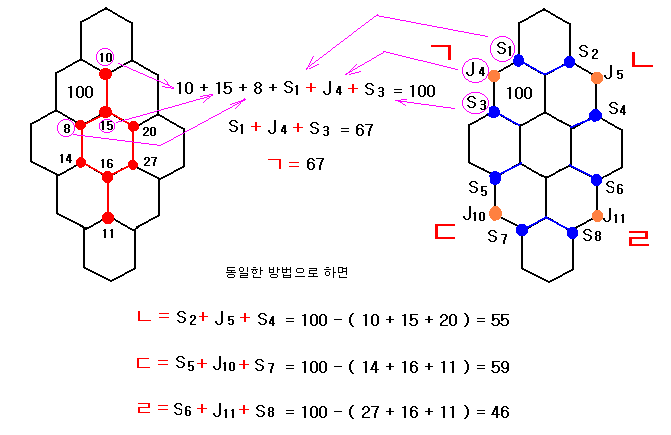
S에서 2개, 텔타에서 한 개를 뽑아 ㄱ,ㄴ,ㄷ,ㄹ 조건에 맞는 숫자들을 아래처럼 모두 나열해 보자.

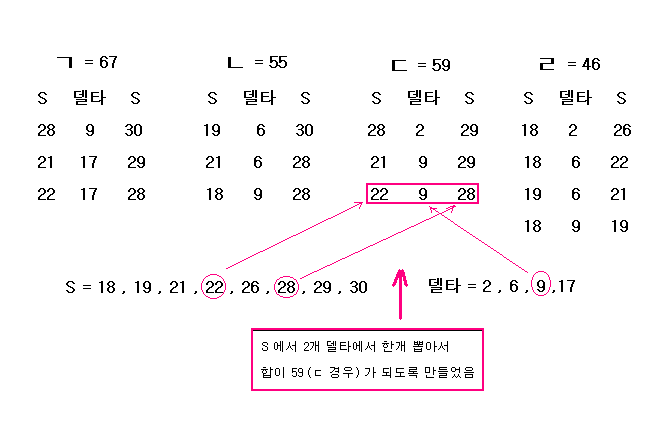
위 처럼 만들어진 ㄱ,ㄴ,ㄷ,ㄹ을 조합하는 경우는 108 가지(3*3*3*4) 나 된다.

하지만 숫자가 서로 겹치는 경우가 있으므로 그것들은 제외해야 한다.

서로 겹치는 숫자가 없도록 ㄱ,ㄴ,ㄷ,ㄹ의 조합을 구해보면 아래처럼 두가지 경우밖에 없다.

           ㄱ                    ㄴ                   ㄷ                  ㄹ

(1)  21   17   29        19   6   30        22   9   28        18   2   26

(2)  22   17   28        19   6   30        21   9   29        18   2   26

위의 두가지가 경우가  S + Jδ 틀이 되며 아래 그림과 같다.

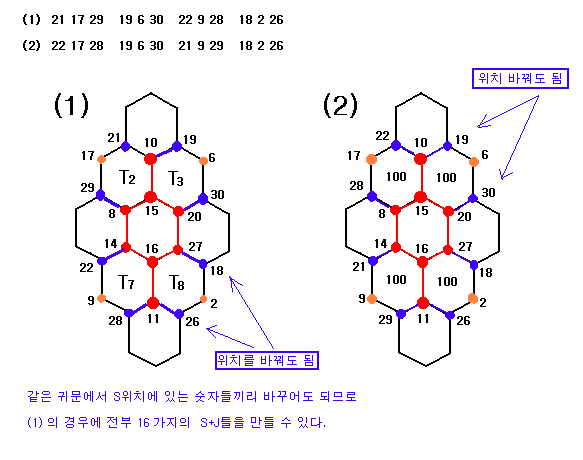
이제 T2, T3 , T7, T8 귀문이 만들어져 지수귀문도의 모양이 거의 다 완성되었다.

한개의 ㄱㄴㄷㄹ조합에서 S의 위치를 바꾸면 총 16 가지의 S+Jδ 틀이 만들어진다.

이 16가지의 틀을 가지고 마지막 단계인 Jε 틀을 만들면 지수귀문도가 탄생한다.

위의 경우에는 (1), (2) 두가지 조합이 있으므로 총 32 가지 S+Jδ 틀이 가능하다.

자 이제 마지막 단계인 Jε 틀을 만들어 보자.