3. 지수귀문도 해를 구하는데 사용된 수학 공식

3-1. CS 공식

지수귀문도의 30개 꼭지점에 1에서 30까지 숫자가 중복됨 없이 하나씩 할당된다.

또한 30개 꼭지점은 C, S, J 중 하나에 반드시 속하므로 아래 식이 성립한다.

   C + S  + J = 1 + 2 + ...... + 30 = 465                          (12)

각각의 귀문에 존재하는 6개 꼭지점의 합은 x 이며 모든 귀문에서 항상 같다.

따라서 9 개의 육각 귀문의 합은 9x 이다.

9 개 귀문의 모든 꼭지점들을 을 더할 때 C 형꼭지점은 3회 , S형 꼭지점은 2회 중복계산되었고

 J 형꼭지점은 1 회 계산되었으므로 아래 식이 성립한다.

          9x = 3C + 2S + J                                              (13)

식(12)와 (13)을 연결해서 식을 변형시켜보자

         9x = 3C + 2S + J

             = 2C + S + C + S + J

             = 2C + S + 465                                            (14)

 따라서, 식(14)를 CS에 관하여 정리하면 CS 공식 (15)가 유도된다.

       2C + S = 9x - 465                                            (15)

위의 식 (15)를 CS 공식이라고 명명한다.

합  x 와 C 꼭지점에 있는 숫자 8개가 결정되면

위 CS 공식에 의해서 S 꼭지점에 존재할 수 있는 8개 숫자들의 합이 결정된다.

합에 맞도록 S 값 8개를 정하면 지수귀문도를 만들 수 있다.

CS 공식을 만족시키지 못하도록 S 값을 정하면 지수귀문도가 만들어지지 않는다.

CS 공식으로 C , S 꼭지점에 할당되는 16개의 숫자들을 임의로 정하면 된다.

그리고 남은 14 개의 숫자가 자동으로 J 에 속하게 될 것이다.

CS공식을 만족하도록 분류된  C, S , J 숫자들을 조건에 맞도록 짝지우면

지수귀문도가 만들어지는데 그 과정이 복잡하고 시간도 많이 걸린다.

복잡한 과정으로 인하여 지수귀문도를 하나 만드는데 대략  1 - 2 시간 걸렸다.

3-2. 베타-델타공식

지수귀문도 만드는 시간을 단축하기 위해서 한개의 공식을 더 만들었다.

이 공식은 유도할 수도 있으나 아래 그림처럼 직관적으로 만들어낼 수 있다.

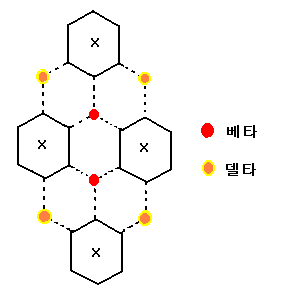
위 그림을 보면 지수귀문도의 30개 꼭지점의 합이 β + δ + 4x 와 같다는 것을 알 수 있다.

따라서   아래 식 (16) 이 성립한다.

           β + δ + 4x = 1 + 2  + .... + 30 = 465                   (16)

(16)식에서 베타-델타 공식(17)가 유도된다.

            β + δ = 465 - 4x                                            (17)                

C형에 속하는 β 와 J형에 속하는 δ는 반드시 위 베타델타공식을 만족하는 숫자들이어야 한다.

베타델타공식을 만족하도록 숫자들은 분류하면 CS공식 하나만 가지고 지수귀문도를 만들 때

발생하는 복잡한 중간과정이 상당히 간단해져서 시간이 많이 단축된다.

30분 이내에 원하는 지수귀문도를 만드는 것이 가능하다.

익숙해지면 더 시간을 단축시킬 수도 있다.