2012년 2월 1일
지수귀문도
1. 최석정 지수귀문도의 모양
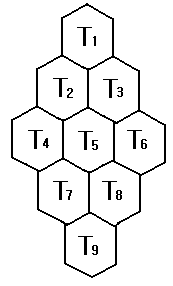
최석정의 지수귀문도는
아홉 개의 정육각형으로 이루어져 있다.
정육각형을 귀문(거북무늬)라고
정의한다.
귀문은 turtle(거북)의 이니셜을
따서 T 라고 명명한다.
각 귀문은 6개 꼭지점을 가진다.
또한 각 귀문은 동일한 합을
가져야 하며 그 합을 x 라고 한다.
아홉 개의 귀문에 위에서 아래로
좌에서 우의 순서를 따라
차례로 번호를 매기면 아래
그림처럼 된다.
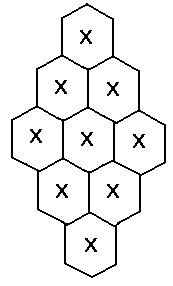
최석정은 x = 93 인 지수귀문도를
만든 것이다.
93 은 6개의 꼭지점들이 모두
평균값을 가질 때의 합에 해당한다.
1 에서 30 까지 30개 숫자의
평균은 15.5 이고 그것이 6개 이면
15.5*6 = 93 이므로 최석정의
지수귀문도가 만들어진다.
최석정이 만든 기책용팔도는
8각 방진인데 1 에서 24까지 24개의 숫자를 사용한다.
1에서 24까지 평균값인 12.5 와 8개의 꼭지점을
곱하면 12.5*8 = 100 이 된다.
그래서 기책용팔도의 합 역시
100 인 것이다.
낙서 49도 1에서 20 까지 20개의
숫자를 사용하고 있으며 그 평균값인 10.5 와 꼭지점 4를 곱하면
10.5*4= 42가 된다. 그래서
낙서 49도의 합도 42 인 것이다.
지수귀문도의 합이 77에서
109가지 33 종류가 존재하지만
합이 93인 지수구문도를 만든
것은
유교가 지배적인 시대에 살던
최석정은 평균값을 중용으로 여겨
가장 안정적인 값이라고 생각했기
때문일 것이다.
2. 꼭지점의 분류
지수귀문도의 일반적인 풀이를
위해서는 꼭지점을 분류하는 것이 필수적이다.
어떤 꼭지점들은 인접한 귀문에
두 번 또는 세 번 겹치기도 한다.
그래서 귀문에 겹치는 횟수를
기준으로 꼭지점들을 세가지로 분류한다.
최석정 이름의 영문이니셜인
C, S, J을 분류 기호로 사용한다.
2-1. C형 꼭지점 ( Core-type
vertex)
세 개의 귀문에 겹쳐있는 꼭지점들을
c형 꼭지점이라고 정의하며 총 8 개가 존재한다.
c형 꼭지점에 위치한 숫자들은
귀문의 합 x 를 구할 때 세 번이나 중복 계산되는 특징을 가진다.
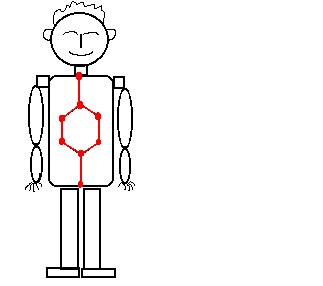
C형 꼭지점들은 지수귀문도의
중심부(core)에 위치하며
사람으로 치면 식도부터 시작해서
위, 장등의 장기와 생식기에 해당한다.
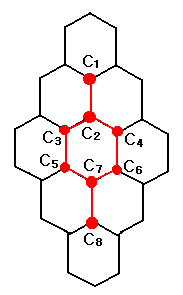
C형에 속하는 8개의 꼭지점에
번호를 매기면 아래 그림과 같다.
이후로는 꼭지점에 위치하는
숫자와 꼭지점의 기호를 동일하게 취급하기로 하자.
즉, C1은 꼭지점 C1을 의미하기도
하지만 동시에 C1에 위치하는 숫자도 뜻한다.
C1에서 C8까지 8개의 꼭지점에
위치하는 숫자들의 합을 C라고 하자
C = C1 + C2 + C3 +
C4 + C5 + C6 + C7 + C8 = 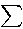 Ci (1) Ci (1)
C형 꼭지점을 다시 세가지로
분류할 수 있다.
첫째, 귀문 T5에 위치하지
않는 2개의 꼭지점 C1 과 C8
이
두 꼭지점의 합을 α 라고 한다.
α
= C1 + C8
(2)
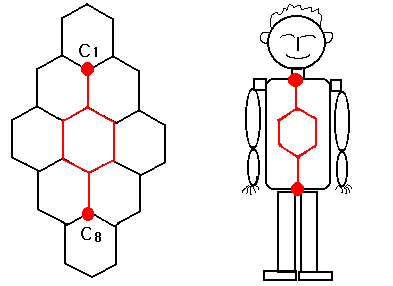
둘째, T5에 위치하면서 중앙에
존재하는 2개의 꼭지점 C2 와 C7
이
두 꼭지점의 합을 β 라고 한다.
β
= C2 + C7
(3)
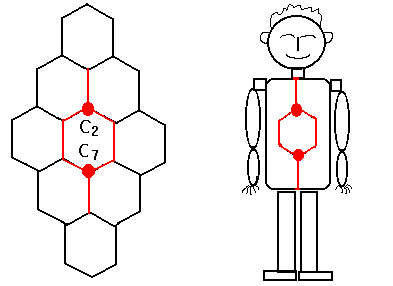
셋째, T5에 위치하면서
좌우 측면에 존재하는 4개의 꼭지점 C3, C4, C5 와 C6
이
네개의 꼭지점의 합을 γ 라고 한다.
γ
= C3 + C4 + C5 + C6
(4)
또한 β 와 γ는 T5 둘레에
있는 6 개의 꼭지점이므로 (6) 식이 성립한다.
β
+ γ = x
(6)
위 세가지를 C형 꼭지점들을
이해하기 쉽게 그림으로 나타내면 아래와 같다.
[
α = C1 + C8 ]
[ β = C2 + C7 ]
[ γ = C3 + C4 + C5 + C6
]
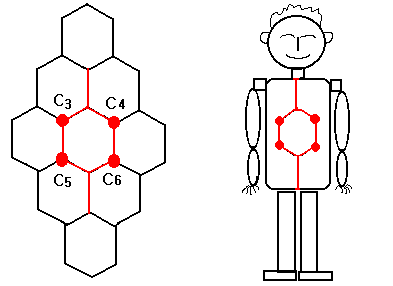
C형 꼭지점에 대해서는 아래와
같은 공식이 성립한다.
C =
α + β + γ = α + x
(7)
|