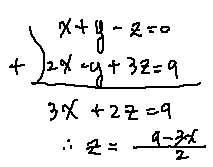7 -3

연 립방 정 식

 

ㅇ 연립방정식 ; 모르는 미지수가 2개 ( x , y )나 3개 ( x , y, z) 인 식이 2개 또는 3개가 있는 방정식

                      연립방정식이 풀리려면 미지수가 2개 일 때 식은 반드시 2개,

                      미지수가 3개일 때 식은 반드시 3개가 필요합니다.

 

ㅇ 연립방정식을 푸는 방법은 다음과 같습니다.

    1. 한 미지수를 없애야 합니다.

    2. 그러기 위해서는 한 미지수에 대하여 정리 후 다음 식에 대입합니다.

    3. 그리곤 마구 풉니다.

 

문1] 다음 연립방정식을 푸시오.

          x  - y = 2                        ---(1)

          x 2  +  y 2   = 10              ---(2)

풀이]  위 식 중에서 (1)식을 변형하면

             x = y  + 2                   ---(3)

       (3)을  (2)식에 대입하면

             (y + 2 ) 2  +  y 2   = y 2  + 4y  + 4  + y 2

                                               =2y 2   + 4y  + 4   =10       ---(4)

      (4)를 정리하면

                 2y 2   + 4y  -6 = 0

                 y 2   + 2y  -3   =0     

                 ( y + 3 ) ( y -1 ) =0

      따라서,  y  = -3  ,  1

           y =  -3 일 때   x = y + 2 = -1

           y =  1  일 때    x = y + 2 = 3

답1]   x  = 3 ,  y  = 1     또는   x = -1 ,  y = -3

 

문2] 다음 연립방정식을 푸시오.

      x + y -z = 0              ---(1)

     2x  - y + 3z =9          ---(2)

     x + 2y + z =8              ---(3)

풀이]  문자를 줄여야 하므로 (1)과 (2)를 더하여 y를 소거(없앰)합니다.

          (1) + (2)를 하면

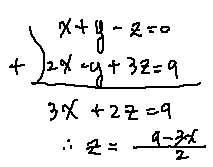              ----(4)

        (1) 과 (3)을 더하여 z를 소거합니다.

        (1) + (3)

           

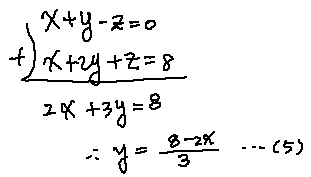
   (4)와 (5)를 가장 간단한 (1)식에 대입하여 계산하면 다음과 같습니다.
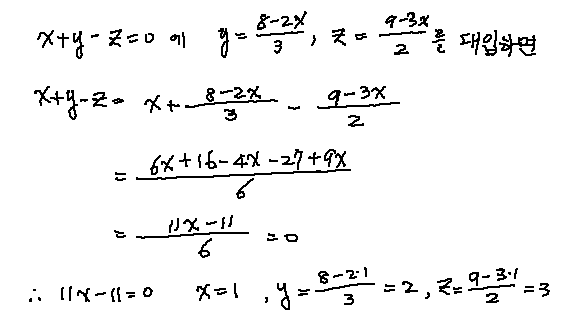