7 -1 |
삼 차 방 정 식 |
ㅇ 3 차 방정식 ; 다음과 같이 표현되는 방정식이 3 차 방정식입니다.;
a x3 + b x 2 + cx + d = 0
ㅇ 3차 방정식은 다음과 같이 풉니다.
1. x 에 1, -1, 2, -2, 3, -3, 4, -4, ....을 차례대로 대입해 봅니다.
2. 대입하고 계산한 결과가 0 이 나오면 그 값은 인수입니다.
예) 1을 대입하였더니 0 이 나왔다면 ( x -1) 이 인수입니다.
-2를 대입하였더니 0 이 나왔다면 (x +2 ) 이 인수입니다.
3. 인수들로 방정식을 나누어 인수분해합니다.
4. 인수분해가 되면 각 인수들은 0 가 되어야 하므로 각 인수들을 0 으로 놓고 계산합니다.
예) ( x + 1 ) ( x - 3 ) ( x - 5 ) = 0 이라면
각 인수인 ( x + 1 ), ( x - 3 ), ( x - 5 ) 은 0 이 되어야 하므로
( x + 1 ) = 0 , ( x - 3 ) = 0 , ( x - 5 ) = 0
따라서, x = -1 , x = 3 , x = 5 입니다.
문1] x3 + 2 x 2 -5 x -6 = 0 를 푸시오.
풀이] x 에 1을 대입하면
1 + 2 -5 -6 = -8 이므로 1 은 탈락
-1 을 대입하면
(-1) + 2 (-1) - 5(-1) -6 =0 이 되죠
따라서, x + 1 은 위 식의 인수가 됩니다.
자, 그럼 다음처럼 나누어 보겠습니다. 보통 나누기 하듯이 하면 됩니다.
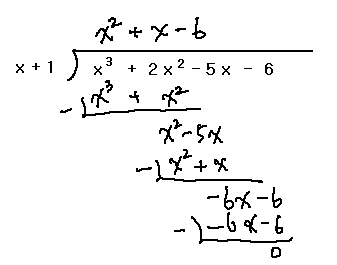
따라서 준 식은 다음처럼 됩니다.
x3 + 2 x 2 -5 x -6 = ( x +1 ) ( x 2 + x -6 )
= ( x + 1 ) ( x +3 ) ( x -2 ) = 0
x = -3, -1 , 2
답] x = -3, -1 , 2