[등가속운동; 가속도>0]
[감속운동; 가속도<0]
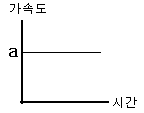
[ 가속도-시간
그래프(a-t)

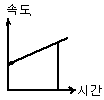
[ 속도 - 시간
그래프(v-t)
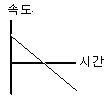
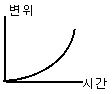
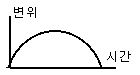
[ 변위-시간
그래프(s-t)
1-5 |
등가속도 운동 |
ㅇ 등가속도 직선운동 ; 일정한 가속도로 일직선 상을 움직이는 운동
ㅇ 중요한 몇가지 공식들
[1] V = Vo + at ( v ; 속도 vo; 처음 속도 a ; 가속도 t ; 시간 ) |
[공식설명] 나중 속도 = 처음 속도 + 늘어난 속도 = 처음 속도 + (가속도 x 시간) |
[2] S = Vo t + ½ at ²( s ; 거리 Vo; 처음 속도 a ; 가속도 t ; 시간 ) |
[공식설명] 간 거리 = 평균속력 x 시간 = (처음속도 + 나중 속도) / 2 x 시간 = [처음속도 + 처음속도 +( 가속도 x 시간 )] / 2 x 시간 = 처음속도 x 시간 + ( 가속도 x 시간 x 시간 ) / 2 |
[3] 2aS = V²- Vo²( s ; 거리 v ; 속도 vo; 처음 속도 a ; 가속도 ) |
[공식설명] 2 x 가속도 x 간 거리 = 나중 속도 제곱 - 처음 속도 제곱 |
ㅇ 여러 가지 그래프들
|
[등가속운동; 가속도>0] |
[감속운동; 가속도<0] |
[ 가속도-시간 그래프(a-t) |
|
|
[ 속도 - 시간 그래프(v-t) |
|
|
[ 변위-시간 그래프(s-t) |
|
|
[문제1] 길이 1 km인 활주로의 한 끝에 정지해있던 비행기가 출발하여 다른 끝에서 100 m/s의
속도로 이륙하였다. [지학사 126쪽]
(1) 비행기가 활주로를 달린 시간은 얼마인가 ?
(2) 비행기가 활주로에서 달릴 때의 평균가속도는 얼마인가 ?
[풀이] (1) 20초 , 비행기가 처음에는 0, 나중에는 100 m/s 이므로 평균 50m/s 의 속도로 달린
셈이다. 활주로의 길이가 1000m 이므로 20초 달린 것이죠. ( 1000 / 50 = 20 )
(2) 5 m/s², 속도가 20초동안 100 m/s나 증가했으므로 가속도는 100/20 = 5 m/s²입니다.
[문제2] 빌딩의 옥상에서 작은 돌을 가만히 놓았더니 3초만에 지면에 도달하였으며 이 때 돌의 속력은
29.4 m/s였다. 3층으로 내려와서 같은 실험을 하였더니 1초가 걸렸다. [지학사 126쪽]
(1) 옥상에서 떨어뜨린 돌의 평균가속도는 ?
(2) 3층에서 옥상까지의 높이는 ?
[풀이] (1) 9.8 m/s², 3초만에 돌의 속력이 29.4 m/s 증가했다. 또한, 가속도 = 증가한 속력 / 시간
이므로 가속도 = 29.4 / 3 = 9.8 m/s²
(2) 39.2 m
|
건물의 높이 = 평균속도 x 걸린 시간. 평균속도는 29.4/2 = 14.7 , 걸린 시간은 3 초이므로 건물 높이 = 14.7 x 3 = 44.1 m 그런데, 3층에서 떨어뜨리면 가속도가 9.8 m/s²이기 때문에 1초 만에 속력은 9.8 m/s 가 된다. 따라서, 평균속도는 4.9 m/s 3층의 높이 = 4.9 x 1 초 = 4.9 m 결국, 3층에서 옥상까지의 높이 = 건물 높이 - 3층 높이 = 44.1 - 4.9 = 39.2 m |