세상은 복잡한 세계죠.

수학 공식도 3차원이상 넘어가면 일반적인 답을 구할 수가 없어요. 내가 어떤 결정을

하려고 해도 벌써 아버지, 어머니, 누나, 동생, 친척, 선생님, 친구 ,애인의 의견을

들어서 결정해야 하니까요. 벌써 8 군데서 의견이 나오는 것입니다. 즉, 8 차원의

풀이가 되는 셈이죠.

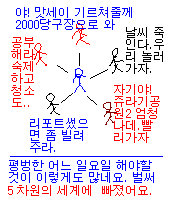
그러므로 우리는 갈팡질팡, 우유부단, 노심초사하는 것입니다. 그 누구의 의견도

필요없이 내 생각대로만하는 단순한 1 차원적인 인간이면 고민, 근심 끝....

단순하게 살기가 얼마나 힘드는데. 세상은 우리를 똑똑하게 만든데니까요.

특히, 한국의 학생들은 입시때문에 얼떨결에 똑똑해졌어요.

미국 대학생 중에 구구단 못하는 애들도 많테니깐요. 한국에서 중간 정도하던

학생이 브라질로 이민을 가서 조금 열심히 공부했더니 그 학교 개교 이래 최고의

점수가 나와 그 브라질 학교의 교장 선생님이 동양에서 천재가 왔다고 야단 법석을

피웠다는 얘기를 들은 적이 있어요.

또한, 얼마전 98년 3월 에 유럽에서 치뤄진 수학경시대회에서 한국의 유학생들이

1, 2위를 하고 10위안에 2명을 배고는 다 한국인 이었다는 기사를 읽었어요.

정말 한국사람들 머리 하나는 죽여준데니까요. 머리가 너무좋아 자기 고집이

강하여 서로 협조하지 않고 헐뜯는 것이 사소한 흠이지만 ...

한국의 모든 젊은이들은 자부심과 자신을 가져도 됩니다.

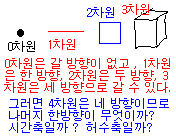
자연현상도 3 가지 이상의 것들이 얽혀있읍니다.

벌써 우리가 사는 세상이 3 차원 아닙니까 ?

날씨 변화만 봐도 기온, 기압, 습도, 구름의 양, 바람 , 수륙의 분포, 도시화 정도등

많은 것을 고려해야 하므로 3 차원으로는 해결이 될 수가 없어요. 그래서, 100 %

정확한 일기예보는 있을 수가 없죠. 인간의 힘으로는 계산을 할 수가 없는 것입니다.

오직 컴퓨터의 힘을 빌려서 대강 예측하는 것이죠.

컴퓨터가 발달하게 된 것이 바로 기상학 때문이라고 해도 과언이 아닙니다.

이렇게 복잡한 혼돈의 세계로 자연이 이루어져 있읍니다. 흔히, 카오스(chaos)의

세계라고도 합니다. 이런 혼돈의 세계를 잘 설명해주는 이론 중 하나가 바로

프랙탈(fractal)이론입니다. 혼돈으로 보이는 세계도 일정한 기본 법칙이 있을

것이다라는 사실은 누구나 짐작할 수 있죠.

이 혼돈의 세계를 풀 수 있는 단서가 발견되었죠. 그것이 바로 프랙탈이론인데

다음과 같은 2 가지 특징이 있어요.

             첫째, 자기유사성 : 자기와 비슷한 것을 만든다.

             둘째, 순환성 : 위의 일을 계속 반복한다.

아주 단순한 이 두가지 법칙을 만족하는 만델브로트집합(1975년 나옴)이 있습니다.

집합하니까 벌써 머리가 찌끈찌끈해지죠. 수학은 괴로워. 그래서 수식없이 설명할테니

두려워 마시압.

만델브로트는 프랑스의 과학자인데 프랙탈이론을 발명(?)했죠. 위 두가지를 만족하는

복소수( 허수가 있은 수 예) 3 + 2 i )를 컴퓨터를 이용해 계산했어요. 만데브로트 집합은

너무나 복잡하여 사람이 도저히 계산할 수 없어요.

그런 이야기도 있잖아요. 옛날 어느 수학자가 평생을 걸려 원주율 파이(3.14)를  

소수점 이하 600(?)몇자리까지 계산했는데  컴퓨터로 단 몇 초동안 계산해보았더니

200(?)몇자리부터 잘못 되었더래요.

그 수학자가 이 사실을 알면 얼마나 황당 + 허무 이겠어요. 일생이 헛수고였으니.

하긴, 이름이라도 남겼으니 우리보다야 백배 낫지만...

만델브로트는 컴퓨터의 계산 결과를 모니터에 그려 보았더니 풍뎅이를 닮은

모양이 나타나는데 이것을 수십배 확대했더니 그 풍뎅이 모양이 다시

나타났어요.(자기유사성) 그것을 또 수십배 확대해보니까 똑같은 모양이

 계속 나타났어요.(순환성)

 다른 부분을 확대해 보면 다른 모양이 계속 나타나는데 해변, 섬, 성게, 공룡등

우주 삼라만상의 모습이 나타나는 것이죠. 이것은 대단한 사건입니다. 우주 만물들이

어쩌면 바로 이런 단순한 원리로 생겨났을지 모르죠. 인간의 유전자가 바로 이런

만델브로트집합에 해당하지 않을까요 ?  부모와 닮으며(자기유사성) 계속 후손을

만드니까(순환성).

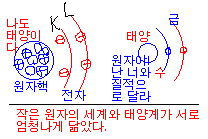
원자핵 주위에 전자가 도는 모습이 태양주위를 돌고 있는 행성들(수,금,지,화,...)과

너무나 닮았어요. 우리 우주가 어쩌면 거인의 콧털속에 있는 원자의 세계일 수도...

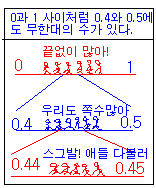
0과 1 사이에 숨어있는 수는 무한대인 것은 다 아시죠. 0.1, 0.2, 0.3, 0.4,....

끝이없어요.  0.1과 0.2 사이에도 0.01, 0.02, 0.03,...등 무한개의 수가 있잖아요.

결국 부분이 전체와  같을 수가 있어요.

작은 모래알 속에 우리 우주와 똑같은 세계가 끊임 없이 반복하고 있을 수도

있다는 얘기죠.

부분 속에 전체가 있다는 것을 잘 보여 주는 예는 많아요. 철수 몸의 작은 세포 속에

들어있는 DNA속에 철수에 관한 모든 정보가 다 들어있어요. 작은 부분 속에 전체가

들어있죠.

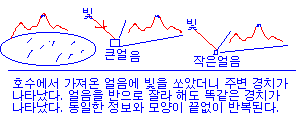
호수에 꽁꽁 언 얼음 한조각(손바닥만한)을 잘러와 거기에 빛을 쏘았더니 반사해서

나온 빛들이 모여 상을 형성하여 호수 주변의 경치를 그대로 보여주었으며,

그 얼음을 반으로 잘라서 빛을 쏘여도 주변 경치가 그대로 나타났다는 연구 결과를

본 적이 있는데 이것도 부분 속의 전체가 아닐까요.

먼 훗날 150억 광년(빛의 속도로 150 억년 가는 거리)이나 되는 우리 우주 밖으로

인류가 나가 보았더니 무엇이 있었을까요. 필자의 소견이지만 어느 초등 학생의

책밖으로 나온 것이 아닐까요. 이 광대한 우주가 어느 초등학생의 책 속에 있는

작은 원자였고 우리 지구인은 그 속에 사는 작은 바이러스였을 뿐....

마찬가지로 아주 작아지는 약을 먹고 책상에 놓인 책속의 원자 세계로 들어 갔더니

우리 인간과 비슷한 생명체가 세번째 전자인 진구에서 잘 난체하고 살고 있는 것을

목격하게 될 지도 모르죠.

진짜 우주는 너무 신비해요.무한대로 작아질 수도 커질 수도 있는 약만 있다면

한번 여행해보고 싶은데. 상상이나 꿈 속에서만 여행하려니 답답해요.

하긴, 우리의 인생도 어쩌면 한여름 밤의 꿈일지로 모르는데....

열심히 삽시다.

너무나 짧고 좁은 세계이지만 ...

여건만되면 지구라는 이 작은 별의 구석 구석까지

다 여행해 보아야 훗날 죽을 때 여한이라도 없지...

에구, 난 언제나 물건너 가보나.